Label Propagation

Supported Graph Characteristics

Unweighted edges

Directed edges

Undirected edges

Homogeneous vertex types

Heterogeneous vertex types

Label Propagation is a heuristic method for determining communities. The idea is simple: If the plurality of your neighbors all bear the label X, then you should label yourself as also a member of X. In effect, this propagates a label from a single vertex to a group of vertices.

The algorithm begins with each vertex having its own unique label. It then iteratively updates labels based on the neighbor influence described above. It is important that the order for updating the vertices be random.

This algorithm is favored for its efficiency and simplicity, but it is not guaranteed to produce the same results every time.

In a variant version, some vertices could initially be known to belong to the same community. If they are well-connected to one another, they are likely to preserve their common membership and influence their neighbors,

Specifications

tg_label_prop (SET<STRING> v_type, SET<STRING> e_type, INT max_iter, INT output_limit,
BOOL print_accum = TRUE, STRING file_path = "", STRING attr = "")

Time complexity

This algorithm has a complexity of \$O(E*k)\$, where \$E\$ is the number of edges and \$k\$ is the number of iterations.

Parameter Description Default

Parameter	Description	Default
`SET<STRING> v_type`	Names of vertex types to use	(empty set of strings)
`SET<STRING> e_type`	Names of edge types to use	(empty set of strings)
`INT max_iter`	Maximum iterations of the algorithm	N/A
`INT output_limit`	Maximum number of vertices to output in JSON format	N/A. Use `-1` to output all vertices.
`BOOL print_accum`	Whether to print data in JSON format to the standard output	False
`STRING attr`	Vertex attribute where community ID values are assigned in `INT` format. No value is assigned if the string is left blank.	(empty string)

SET<STRING> v_type

Names of vertex types to use

(empty set of strings)

SET<STRING> e_type

Names of edge types to use

(empty set of strings)

INT max_iter

Maximum iterations of the algorithm

N/A

INT output_limit

Maximum number of vertices to output in JSON format

N/A. Use -1 to output all vertices.

BOOL print_accum

Whether to print data in JSON format to the standard output

False

STRING attr

Vertex attribute where community ID values are assigned in INT format. No value is assigned if the string is left blank.

(empty string)

Output

Assigns a component ID in INT format to each vertex. Members of the same component have the same ID value.

Result size

The result size is calculated by \$V\$, the number of vertices.

Example

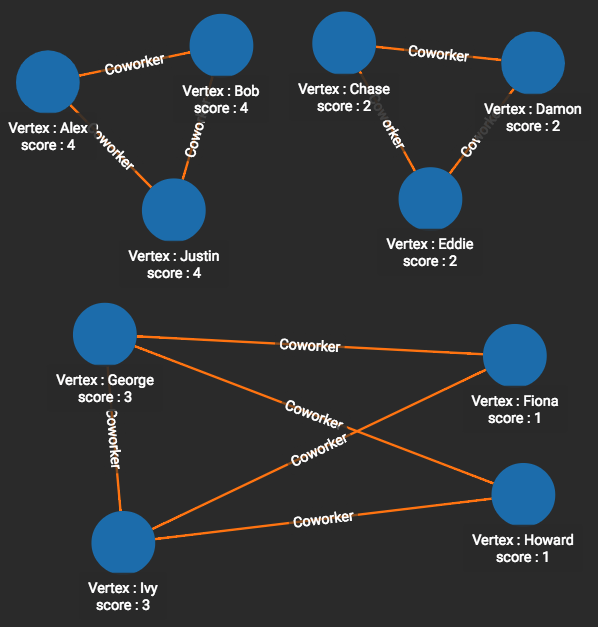
This is the same graph that was used in the Connected Component example. The results are different, though. The quartet of Fiona, George, Howard, and Ivy have been split into 2 groups:

(George & Ivy) each connect to (Fiona & Howard) and to one another.
(Fiona & Howard) each connect to (George & Ivy) but not to one another.

Label Propagation tries to find natural clusters and separations within connected components. That is, it looks at the quality and pattern of connections. The Connected Component algorithm simply asks the Yes or No question: Are these two vertices connected?

We set max_iter to 10, but the algorithm reaches a steady state after 3 iterations:

# Use _ for default/empty values
RUN QUERY tg_label_prop(["Person"], ["Coworker"], 10, -1, _, _, _)

Visualized results of example query on social10 graph with Coworker edges