ArticleRank

Supported Graph Characteristics

Unweighted edges

Directed edges

Homogeneous vertex types

ArticleRank is an algorithm that has been derived from the PageRank algorithm to measure the influence of journal articles.

Page Rank assumes that relationships originating from low-degree vertices have a higher influence than relationships from high-degree vertices. Article Rank keeps the PageRank methodology but modifies the formula to lower the influence of low-degree nodes.

The Article Rank of a node \(v\) at iteration \(i\) is defined as:

\[ArticleRank_i(v) = (1-d) + d \sum_{w\in N_{in}(v)} \frac{ArticleRank_{i-1}(w)}{|N_{out}(w)| + \overline{N_{out}}}\]

Within the formula:

\(N_{in}(v)\) are the incoming neighbors and \(N_{out}(v)\) are the outgoing neighbors of node \(v\).
\(d\) is a damping factor in [0, 1], usually set to 0.85.
\(\overline{N_{out}}\) is the average outdegree.

Notes

For more information, see ArticleRank: a PageRank‐based alternative to numbers of citations for analysing citation networks.

Specifications

CREATE QUERY tg_article_rank (STRING v_type, STRING e_type,
 FLOAT max_change=0.001, INT max_iter=25, FLOAT damping=0.85, INT top_k = 100, BOOL print_accum = TRUE, STRING result_attr =  "", STRING file_path = "")

Parameters

Name Description

Name	Description
`STRING v_type`	A vertex type.
`STRING e_type`	An edge type.
`FLOAT max_change`	Article Rank will stop iterating when the largest difference between any vertex’s current score and its previous score ≤ `max_change.` That is, the scores have become very stable and are changing by less than `max_change` from one iteration to the next.
`INT max_iter`	Maximum number of iterations.
`FLOAT damping`	The damping factor. Usually set to 0.85.
`INT top_k`	The number of results with the highest scores to return.
`BOOL print_accum`	If true, print JSON output.
`STRING result_attr`	If not empty, store the article rank score of each vertex in this attribute.
`STRING file_path`	If not empty, write output to this file.

STRING v_type

A vertex type.

STRING e_type

An edge type.

FLOAT max_change

Article Rank will stop iterating when the largest difference between any vertex’s current score and its previous score ≤ max_change. That is, the scores have become very stable and are changing by less than max_change from one iteration to the next.

INT max_iter

Maximum number of iterations.

FLOAT damping

The damping factor. Usually set to 0.85.

INT top_k

The number of results with the highest scores to return.

BOOL print_accum

If true, print JSON output.

STRING result_attr

If not empty, store the article rank score of each vertex in this attribute.

STRING file_path

If not empty, write output to this file.

Output

Returns the article rank score for each vertex in descending order.

Result size

The result size is equal to \(V\), the number of vertices, because one score is produced for every vertex in the graph.

Time complexity

The algorithm has a time complexity of \(O(E*k)\), where \(E\) is the number of edges and \(k\) is the number of iterations.

The number of iterations is data-dependent, but the user can set a maximum. Parallel processing reduces the time needed for computation.

Example

Suppose we have the following graph:

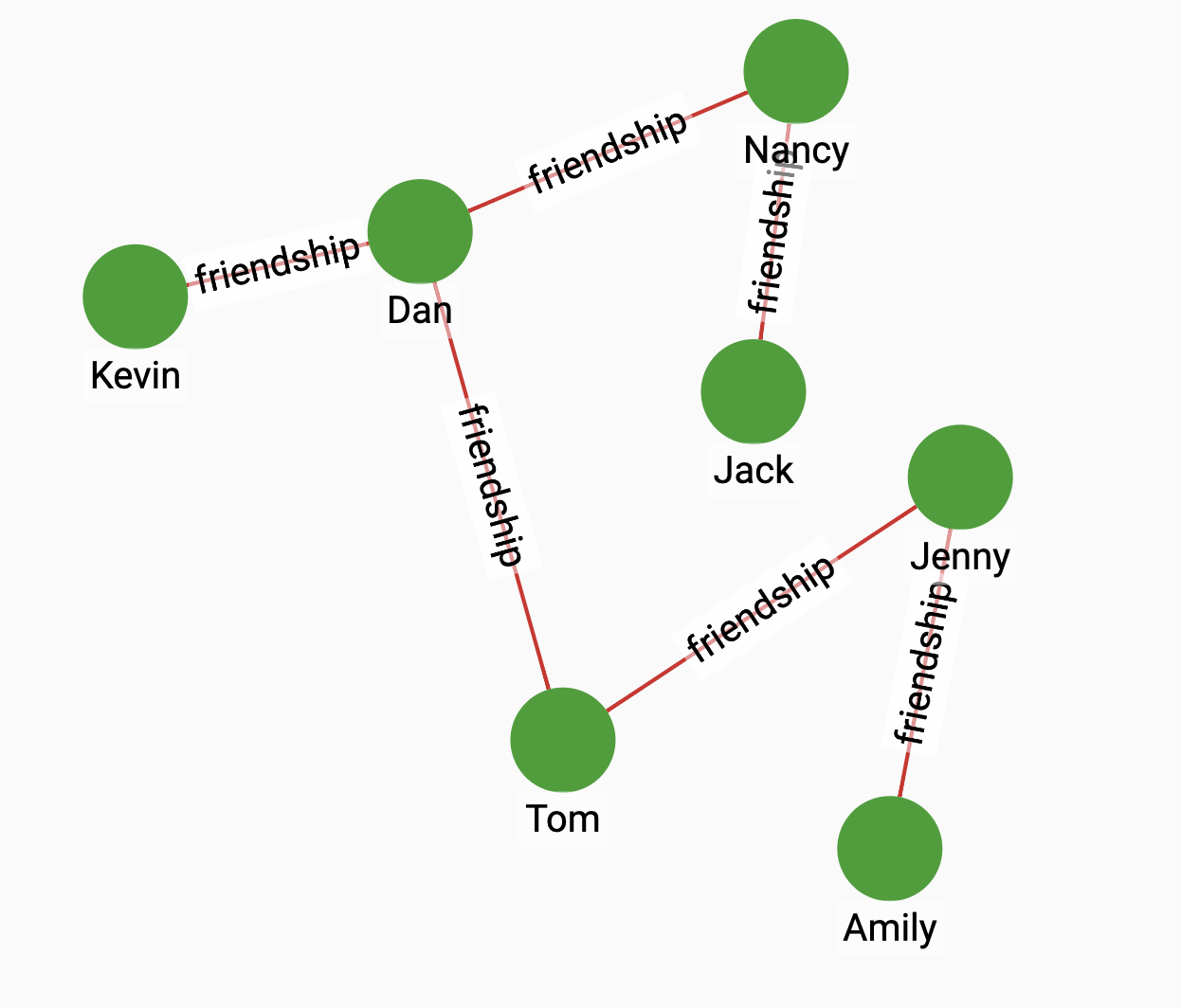
By running Article Rank on the graph, we will see that the vertex with the highest score is Dan:

Query
Result

RUN QUERY tg_article_rank ("person", "friendship", _, _, _, _, _)

{
  "error": false,
  "message": "",
  "version": {
    "schema": 2,
    "edition": "enterprise",
    "api": "v2"
  },
  "results": [{"@@topScores": [
    {
      "score": 2348294.75,
      "Vertex_ID": "Dan"
    },
    {
      "score": 1863160.625,
      "Vertex_ID": "Jenny"
    },
    {
      "score": 1442890.5,
      "Vertex_ID": "Tom"
    },
    {
      "score": 1053484.625,
      "Vertex_ID": "Nancy"
    },
    {
      "score": 739327.9375,
      "Vertex_ID": "Kevin"
    },
    {
      "score": 703562.75,
      "Vertex_ID": "Amily"
    },
    {
      "score": 498013.25,
      "Vertex_ID": "Jack"
    }
  ]}]
}