Degree Centrality

Supported Graph Characteristics

Unweighted edges

Directed edges

Undirected edges

Homogeneous vertex types

Heterogeneous vertex types

Degree centrality is defined as the number of edges incident upon a vertex (i.e., the number of ties that a node has).

One major application of degree centrality is in cybersecurity, and more generally, network management.

The degree can be interpreted in terms of the immediate risk of a node for catching whatever is flowing through the network (such as a virus, or some information).

Specifications

CREATE QUERY tg_degree_cent(SET<STRING> v_type, SET<STRING> e_type,
  SET<STRING> re_type, BOOL in_degree = TRUE, BOOL out_degree = TRUE,
  INT top_k=100, BOOL print_accum = True, STRING result_attr = "",
  STRING file_path = "")

Parameters

Name Description Default value

Name	Description	Default value
`SET<STRING> v_type`	A set of vertex types.	(empty set of strings)
`SET<STRING> e_type`	A set of edge types.	(empty set of strings)
`SET<STRING> re_type`	A set of reverse edge types. If an edge is undirected, put the edge name in the set as well.	(empty set of strings)
`BOOL in_degree`	Boolean value that indicates whether to count the incoming edges as part of a vertex’s degree centrality.	True
`BOOL out_degree`	Boolean value that indicates whether to count the outgoing edges as part of a vertex’s degree centrality.	True
`INT top_k`	The number of vertices with the highest scores to return.	100
`BOOL print_accum`	If true, print results to JSON output.	True
`STRING result_attr`	If not empty, save the degree centrality score of each vertex to this attribute.	(empty string)
`STRING file_path`	If not empty, save results in CSV to this file.	(empty string)

SET<STRING> v_type

A set of vertex types.

(empty set of strings)

SET<STRING> e_type

A set of edge types.

(empty set of strings)

SET<STRING> re_type

A set of reverse edge types. If an edge is undirected, put the edge name in the set as well.

(empty set of strings)

BOOL in_degree

Boolean value that indicates whether to count the incoming edges as part of a vertex’s degree centrality.

True

BOOL out_degree

Boolean value that indicates whether to count the outgoing edges as part of a vertex’s degree centrality.

True

INT top_k

The number of vertices with the highest scores to return.

100

BOOL print_accum

If true, print results to JSON output.

True

STRING result_attr

If not empty, save the degree centrality score of each vertex to this attribute.

(empty string)

STRING file_path

If not empty, save results in CSV to this file.

(empty string)

Output

The vertices with the highest degree centrality scores along with their scores.

Time complexity

The algorithm has a time complexity of \(O(E)\), where \(E\) is the total number of edges in the graph.

Example

Suppose we have the following graph:

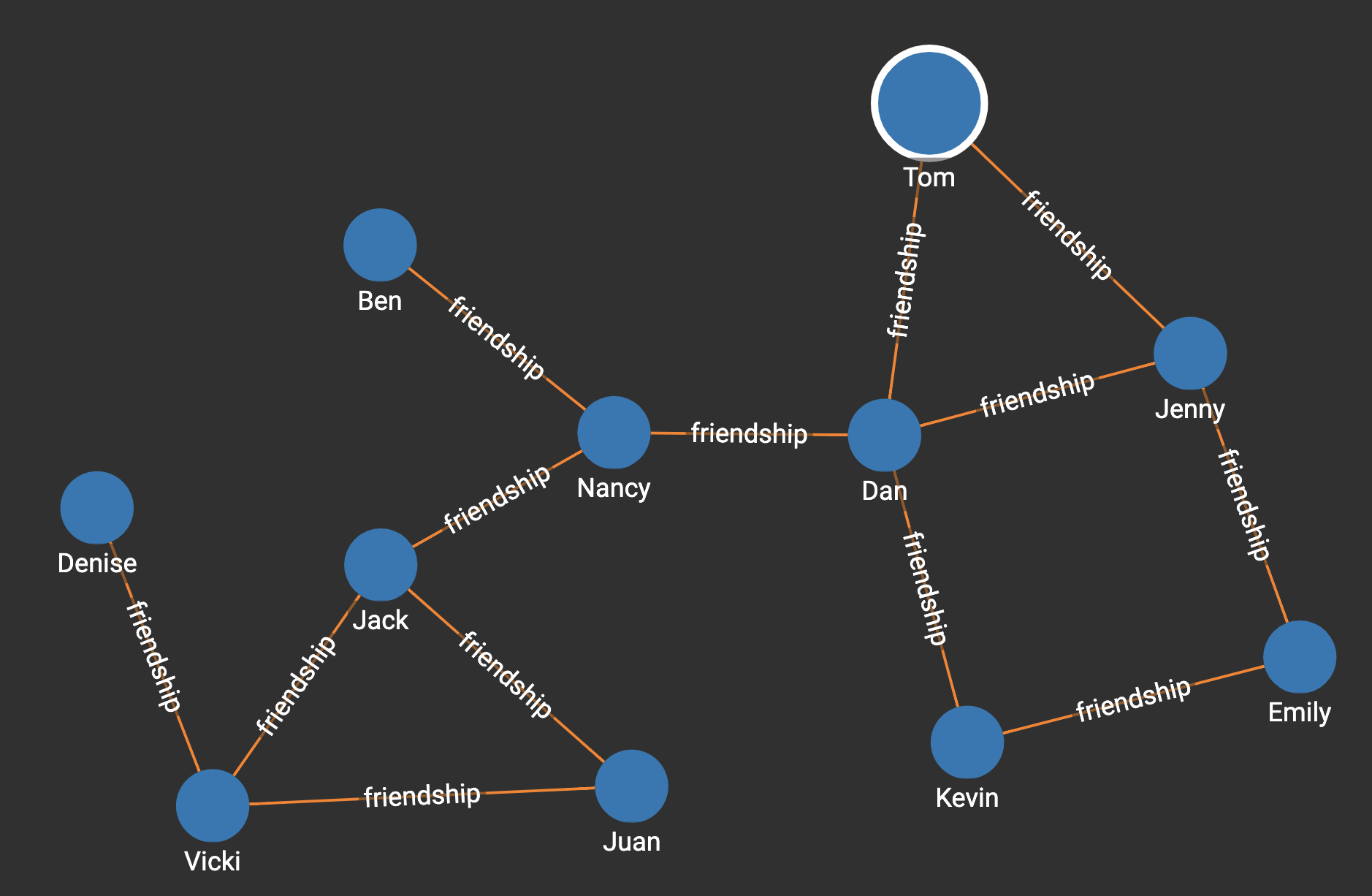
Running the query on the graph will show that Dan has the highest degree centrality:

Query
Result

RUN QUERY tg_degree_cent(["person"], ["friendship"],["friendship"])

[
  {
    "top_scores": [
      {
        "Vertex_ID": "Dan",
        "score": 4
      },
      {
        "Vertex_ID": "Jenny",
        "score": 3
      },
      {
        "Vertex_ID": "Nancy",
        "score": 3
      },
      {
        "Vertex_ID": "Vicki",
        "score": 3
      },
      {
        "Vertex_ID": "Jack",
        "score": 3
      },
      {
        "Vertex_ID": "Juan",
        "score": 2
      },
      {
        "Vertex_ID": "Emily",
        "score": 2
      },
      {
        "Vertex_ID": "Kevin",
        "score": 2
      },
      {
        "Vertex_ID": "Tom",
        "score": 2
      },
      {
        "Vertex_ID": "Denise",
        "score": 1
      },
      {
        "Vertex_ID": "Ben",
        "score": 1
      }
    ]
  }
]