PageRank

Supported Graph Characteristics

Unweighted edges

Directed edges

Undirected edges

Homogeneous vertex types

Algorithm links: PageRank

The PageRank algorithm measures the influence of each vertex on every other vertex. PageRank influence is defined recursively: a vertex’s influence is based on the influence of the vertices which refer to it. A vertex’s influence tends to increase if either of these conditions are met:

It has more referring vertices
Its referring vertices have higher influence

The analogy to social influence is clear.

A common way of interpreting PageRank value is through the Random Network Surfer model. A vertex’s PageRank score is proportional to the probability that a random network surfer will be at that vertex at any given time. A vertex with a high PageRank score is a vertex that is frequently visited, assuming that vertices are visited according to the following Random Surfer scheme:

Assume a person travels or surfs across a network’s structure, moving from vertex to vertex.
The surfer can start anywhere. This start-anywhere property is part of the magic of PageRank, meaning the score is a truly fundamental property of the graph structure itself.
Each round, the surfer randomly picks one of the outward connections from the surfer’s current location. The surfer repeats this random walk for a long time.
There is a small probability that the surfer’s next step will be a random vertex instead of a connected vertex. This probability is expressed in the algorithm as (1 - damping).

Notes

For more information, see the Google paper on PageRank.

Specifications

tg_pagerank (STRING v_type, STRING e_type,  FLOAT max_change=0.001, INT max_iter=25, FLOAT damping=0.85, INT top_k = 100,   BOOL print_accum = TRUE, STRING result_attr =  "", STRING file_path = "",   BOOL display_edges = FALSE)

Parameters

Parameter Description Default

Parameter	Description	Default
`STRING v_type`	Names of vertex type to use	(empty string)
`STRING e_type`	Names of edge type to use	(empty string)
`FLOAT max_change`	PageRank will stop iterating when the largest difference between any vertex’s current score and its previous score ≤ `max_change.` That is, the scores have become very stable and are changing by less than `max_change` from one iteration to the next.	0.001
`INT max_iter`	Maximum number of iterations.	25
`FLOAT damping`	Fraction of score that is due to the score of neighbors. The balance (1 - damping) is a minimum baseline score that every vertex receives.	0.85
`INT top_k`	Sort the scores highest first and output only this many scores	100
`BOOL print_accum`	If True, output JSON to standard output	True
`STRING result_attr`	If not empty, store PageRank values in `FLOAT` format to this vertex attribute	(empty string)
`STRING file_path`	If not empty, write output to this file.	(empty string)
`BOOL display_edges`	If true, include the graph’s edges in the JSON output, so that the full graph can be displayed.	False

STRING v_type

Names of vertex type to use

(empty string)

STRING e_type

Names of edge type to use

(empty string)

FLOAT max_change

PageRank will stop iterating when the largest difference between any vertex’s current score and its previous score ≤ max_change. That is, the scores have become very stable and are changing by less than max_change from one iteration to the next.

0.001

INT max_iter

Maximum number of iterations.

FLOAT damping

Fraction of score that is due to the score of neighbors. The balance (1 - damping) is a minimum baseline score that every vertex receives.

0.85

INT top_k

Sort the scores highest first and output only this many scores

100

BOOL print_accum

If True, output JSON to standard output

True

STRING result_attr

If not empty, store PageRank values in FLOAT format to this vertex attribute

(empty string)

STRING file_path

If not empty, write output to this file.

(empty string)

BOOL display_edges

If true, include the graph’s edges in the JSON output, so that the full graph can be displayed.

False

Output

Computes a PageRank FLOAT value for each vertex and stores it in a specified attribute on each vertex.

Time complexity

This algorithm has a time complexity of \$O(E*k)\$ where \$E\$ is the number of edges and \$k\$ is the number of iterations.

The number of iterations is data-dependent, but the user can set a maximum. Parallel processing reduces the time needed for computation.

Example

 # Use _ for default values
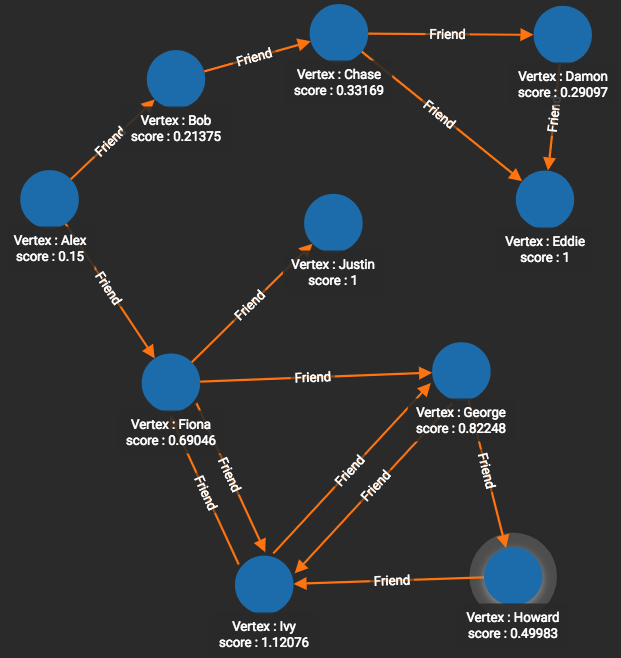
RUN QUERY tg_pagerank("Person", "Friend", 0.001, 25, 0.85, 100 _, _, _, _)

We ran PageRank on our test10 graph (using Friend edges) with the following parameter values:

damping=0.85
max_change=0.001
max_iter=25

We see that Ivy (center bottom) has the highest PageRank score (1.12). This makes sense since there are 3 neighboring persons who point to Ivy, more than for any other person. Ivy’s high PageRank score indicates that Ivy is a relatively important person in this social group.

Eddie and Justin have scores of exactly 1 because they do not have any out-edges. This is an artifact of our particular version of PageRank. Likewise, Alex has a score of 0.15. This comes from (1 - damping), because Alex has no in-edges, meaning that Alex could only have been reached by a random visit rather than a directed connection.

Visualized results of example query on social10 graph