Weakly Connected Components

Supported Graph Characteristics

Unweighted edges

Homogeneous vertex types

Heterogeneous vertex types

Algorithm link: Weakly Connected Components

In a graph, there may not always be connections between every vertex and every other vertex. In some cases, there may be components, which are defined as connected subgraphs that are not connected to other subgraphs.

A connected component is the maximal set of connected vertices inside a graph, plus their connecting edges. Inside a connected component, you can reach each vertex from each other vertex.

Graph theory distinguishes between strong and weak connections:

  • A subgraph is strongly connected if it is directed and if every vertex is reachable from every other following the edge directions.

  • A subgraph is weakly connected if it is undirected or if the only connections that exist for some vertex pairs go against the edge directions.

This Weakly Connected Components algorithm runs on graphs with undirected edges and finds connected components. It assigns a component ID to each vertex. Vertices in the same component get the same component ID.

This algorithm can be used as a helper algorithm to find existing communities and create community IDs before other algorithms are run on the graph.

Illustration

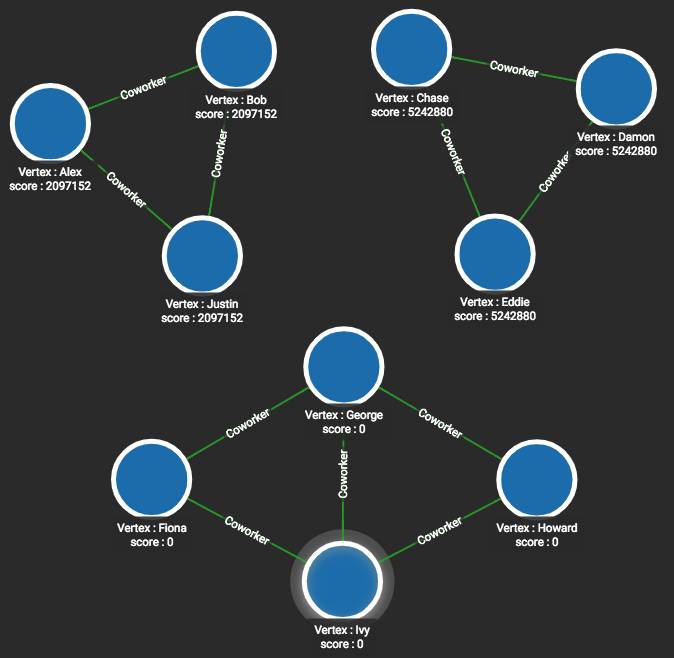
There are three components in the following figure. The score attribute for each vertex is equivalent to the community ID.

Visualized results of example query on social10 graph with Coworker edges

Specifications

CREATE QUERY tg_wcc (SET<STRING> v_type, SET<STRING> e_type, INT output_limit = 100,
    BOOL print_accum = TRUE, STRING result_attr = "", STRING file_path = "")

Time complexity

This algorithm has a time complexity of \$O(E*d)\$, where \$E\$ is the number of edges and \$d\$ is the maximum component diameter.

Space complexity

This algorithm has a space complexity of \$O(V)\$, where \$V\$ is the number of vertices.

Memory usage

There are no special memory considerations for this algorithm.

Output

Assigns a component ID (INT) to each vertex, such that members of the same component have the same id value.

The return value in JSON includes all vertices and the component they belong to, as well as a map of the components with their ID and size.

Parameters

Parameter Description Default

SET<STRING> v_type

Names of vertex types to use

(empty set of strings)

SET<STRING> e_type

Names of edge types to use

(empty set of strings)

INT output_limit

The maximum number of vertices to output in JSON format. Use -1 for an unlimited value.

100

BOOL print_accum

Whether to print the JSON to the standard output.

False

STRING result_attr

The vertex attribute where community ID values will be stored. Must be of type INT.

(empty string)

STRING file_path

If not empty, write the output to this file.

(empty string)

Example

RUN QUERY tg_wcc(["Person"], ["Coworker"], _, _, _, _)

It is easy to see in this small graph that the algorithm correctly groups the vertices:

  • Alex, Bob, and Justin all have Community ID = 2097152

  • Chase, Damon, and Eddie all have Community ID = 5242880

  • Fiona, George, Howard, and Ivy all have Community ID = 0

Our algorithm uses the TigerGraph engine’s internal vertex ID numbers. Currently there is no ability to customize the community IDs.

Visualized results of example query on social10 graph with Coworker edges